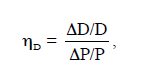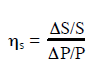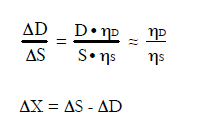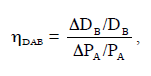Level of analysis: Micro and meso level.
Assessed aspects of sustainability: All; the PEM results can be part of the assessment of all aspects of sustainability.
Main purpose of the assessment:
To predict and quantify effects of decisions on the price and flow of specific materials, products and services.
Description of the methodology:
PEM is a technique for modelling the markets of selected goods (materials, products and/or services). It utilised either explicit supply and demand curves, or estimates of how sensitive the supply and demand are for changes in the price of the good. It can also account for effects of changes in the price of related goods.
Detailed Description
The concept of partial equlibrium is based on the idea of supply and demand being kept in balance through changes in price. If a decision results in an increased use (ΔX ) of a material, product or service in a life cycle, this will contribute to an increase in the price of this good. This increase is likely to stimulate increased production (S) of the good, but also to reduce the demand (D) for the good in other life cycles. Such effects can be quantified through partial equilibrium modelling (PEM).
PEM can be applied on the conceptual level as well as in optimising computer models. On the conceptual level, effects on supply and demand are quantified through estimates of price elasticity. The own-price elasticity of demand (ηD) can be defined as follows (Friedman 1976):
where DD is the estimated change in demand resulting from a change in price (DP) . This estimate is often calculated from time series over the development of price and demand. hD is generally a negative number.
An own-price elasticity of supply (hS)can be defined in a similar way:
For marginal changes in the market of the good (i.e., DX<<D ≈ S) the effects on the production of the good, and on the demand for the good in other life cycles, can be calculated from the own-price elasticity of supply and demand using the following equations (Ekvall 2000):
When the demand for the good in other life cycles is affected, this can also affect the use of other goods in these systems. As an example, Ekvall & Andrae (2006) assumed the alternative use of lead to be in batteries in remote areas, allowing for an increase in the use of photovoltaics and replacing diesel generators. Through PEM, effects on the use of other products can be quantified using estimates of the cross-price elasticity of demand (hDAB):
where DDB is the estimated change in demand for good B resulting from a change in the price of good A (DPA). hDAB is generally a positive number for competing products, but a negative number for complementary products.
Partial equilibrium models is an established tool in the area of environmental economics. It has been used to assess the environmental consequences of policy decisions and other strategic decisions. However, the studies are often restricted to effects on CO2 emissions from the energy sector (Nakata 2000, Nakata & Lamont 2001). An exception is Savard (2000), who used a partial equilibrium model to investigate nitrate and phosphate emissions to water from Canadian pork production. None of these studies has the comprehensive scope on environmental impacts that is typical for LCA.
Optimising computer models of energy systems often include explicit supply curves that describe how the marginal running cost of energy supply increases with the quantity delivered at a given moment or period in time. The demand for energy is sometimes exogenously fed into the model (e.g., Knutsson et al. 2006), but the demand can also be modelled through own-price elasticity estimates, demand curves, or cost curves for energy efficiency measures (e.g., Unger 2003). This means that the supply and demand on the energy markets are in balance in the optimum identified by the model. Optimising energy systems models with partial equilibrium includes, for example, the global model POLES (Criqui 1996), the EU-15 model PRIMES (Capros et al. 1997), and different versions of MARKAL (Fishbone & Abilock 1981), particularly MARKAL-ED (Loulou & Lavigne 1995) and MARKAL-MICRO (van Regemorter & Goldstein 1995).
Strengths
In a traditional LCA model, the unit processes are directly connected by physical flows. By introducing partial economic models, the LCA model accounts for the fact that these physical flows are traded on a market. An increase in the use of a good in the life cycle typically can contribute to increasing the market price of this good. This not only stimulates the production of the good, but also reduces the use of the good in other life cycles. PEM describes both of these effects. This is particularly valuable in a consequential LCA: it makes the description and analysis of the consequences more comprehensive and accurate.
The fact that PEM is a well-known tool in its own right is a strength. It makes it easier to communicate and describe the method when PEM is integrated into an LCA. It also contributes to the credibility of case studies where the integrated method is applied.
The fact that PEM is established in the area of environmental economics means that there are people with an expertise in PEM as well as environmental issues. These can be practitioners, supervisors and/or supervisors in case studies where PEM is integrated into LCA.
Weaknesses/Limitations
The large uncertainty in price elasticity estimates, demand curves and, to some extent, supply curves means that PEM results are highly uncertain. For the price elasticity of supply of old newsprint, the literature includes estimates ranging at last from 0.06 to 1.70 (Palmer et al. 1997). The large difference between these estimates may depend on errors in individual estimates, but is, to some extent, caused by case specific factors such as the time and place where the material is collected for recycling. The price elasticities depend on, e.g., the collection schemes and the legislation that are implemented at that time and location.
Price elasticities also vary with the time-horizon: in the long-term perspective, the buyers are able to adapt to changes in the price when making investments. Hence, the demand is in general more elastic in a long-run perspective than in a short-run perspective (Friedman 1976, Nestor 1992). The elasticity of supply can also be expected to be higher in a long-run perspective than in a short-run perspective (Edwards 1979). As indicated by Weidema et al. (1998), long-run effects are relevant in most LCAs. Unfortunately, the long-run elasticity is typically more difficult to calculate from time series than the short-run elasticity.
Partial equilibrium modelling can be expected to require economists. Even if there are researchers with a combined expertise in PEM and environmental issues, they are not currently part of the LCA community. Economists with relevant expertise are typically not readily available to LCA practitioners.
Partial equilibrium modelling also adds to the complexity and cost of the LCA. When the complexity increases, the risk for calculation errors and other mistakes also increases. The study also becomes more difficult to interpret and report in a transparent manner.
Introducing partial equilibrium models in LCA becomes more feasible, and much less costly, if own-price elasticities from the literature can be used in case studies. Using literature data increases the uncertainty, however, since own-price elasticities depend on case-specific factors such as the time, place, and time horizon.
The cost and complexity can both be reduced by focussing on the parts of the technological and economic system where the most important consequences are expected to occur. This means that the life cycle model is reduced to include only the flows and processes where changes are expected to be important for the results and conclusions, and that partial equilibrium models are added only when effects on other life cycles are expected to be very important for the results and conclusions.
This solution has the weakness that the LCA will depend more heavily on what is expected to be important in advance of the study. This problem is probably general: when more impact categories and/or causal mechanisms are added to the LCA methodology, each study can afford to include fewer aspects that are expected to be insignificant.
Opportunities for broadening and deepening LCA
The increasing interest in consequential LCA offers an opportunity for introducing PEM in LCA case studies. Integrating PEM in LCA can, hence, be regarded as an attractive step forwards for practitioners, decision-makers and stakeholders with an interest in LCAs that describe the consequences of potential decisions (Ekvall et al. 2005a).
The more general methodology of Impact Assessment also provides an opportunity for PEM in LCA. Practitioners and commissioners of Impacts Assessments might consider the focus of LCA on individual product life cycles too narrow. With PEM, the LCA explicitly accounts for indirect effects in other life cycles. This broader scope might make LCA a more attractive tool for Impact Assessments.
The combination of PEM and LCA would be made more feasible if the price elasticity of demand and supply is estimated for more products. To make the estimates available to LCA practitioners, they should be compiled in databases that are posted in connection to ordinary LCI databases.
Threats for broadening and deepening LCA
While potentially very interesting for consequential LCA, PEM is hardly relevant at all for attributional LCA. Most performed LCA can probably still be best described as attributional case studies. Ekvall et al. (2005b) argue that the continued use of attributional LCA can be defended because of the uncertainties and practical problems of consequential LCA, and because a widespread use of consequential LCA can also have unwanted environmental consequences in terms of sub-optimised systems. In addition, practitioners, decision-makers and stakeholders may well consider the results of a consequential LCA unfair, because producers that initiate and maintain good production systems might not get any credit from this in the consequential LCA.
Literature/Internet links
Capros P, Mantzos L, Kolokotsas D, Ioannou N, Georgakopoulos T, Filippopoulitis A, Antoniou Y, Van Regemorter D, Proost S, Lantz F, Saint-Antonin V, Babusiaux D, Smeers Y, Canon E, Schlenzig C. (1997) The PRIMES Energy System Model – Reference Manual. National Technical University of Athens, Greece. url: http://www.e3mlab.ntua.gr.
Criqui P. (1996) POLES 2.2. – Reference Guide. Institute d’Économie et de Politique de Grenoble, France.
Edwards R. (1979) Price expectations and the supply of wastepaper. J. Environ. Econom. Manage. 6:332-340.
Ekvall T. (2000) A market-based approach to allocation at open-loop recycling. Resources, Conservation and Recycling 29(1-2):93-111.
Ekvall T, Andrae A. (2006) Attributional and consequential environmental assessment of the shift to lead-free solders. Int. J. LCA 11(5):344-353.
Ekvall T, Mattsson N, Münter M. (2005a) System-wide environmental consequences of Vistar combustion in Stenungsund – Feasibility study. Report 2005:1. Division of Energy Technology, Chalmers University of Technology, Gothenburg, Sweden.
Ekvall T, Tillman A-M, Molander S. (2005b) Normative ethics and methodology for life cycle assessment. J. Cleaner Prod. 13(13-14):1225-1234.
Fishbone LG, Abilock H. (1981) MARKAL, a Linear-programming Model for Energy Systems Analysis: Technical Description of the BNL Version. Energy Research 5:353-375.
Friedmand M. (1976) Price Theory. Aldine Publishing Company, Chicago, USA.
Knutsson D, Sahlin J, Werner S, Ekvall T, Ahlgren EO. (2006) HEATSPOT – a simulation tool for national district heating analyses. Energy 31(2-3):278-293.
Loulou R, Lavigne D. (1995) “MARKAL model with elastic demands: Application to greenhouse gas emission control”. In Carraro C. and Haurie A. (eds.) Operations research and environmental management. Kluwer Academic Publishers, ISBN: 0-7923-3767-0.
Nakata T. (2000) Analysis of the impact of hybrid vehicles on energy systems in Japan. Transp. Res. D: Transp. Environ. 5D(5):373-383.
Nakata T, Lamont A. (2001) Analysis of the impacts of carbon taxes on energy systems in Japan. Energy Policy 29(2):159-166.
Nestor DV. (1992) Partial Static Equilibrium Model for Newsprint Recycling. Applied Economics 24:411-417.
Palmer K, Sigman H, Walls M. (1997) The Cost of Reducing Municipal Solid Waste. J. Environ. Econom. Manage. 33:128-150.
Savard M. (2000) Modelling risk, trade, agricultural and environmental policies to assess trade-offs between water quality and welfare in the hog industry. Ecol. Model. 125(1):51- 66.
Unger T. (2003) Common energy and climate strategies for the Nordic countries. PhD thesis. Dept. of Energy Technology, Chalmers University of Technology, Gothenburg, Sweden.
Van Regemorter D, Goldstein G. (1995) MARKAL-MICRO – Development of MARKAL towards a partial equilibrium model. ETSAP Technical Paper. ETSAP Operating Agent Prof. E. Lavagno, Politechnico di Torino, Torino, Italy. url:
www.etsap.org.
Weidema BP, Frees N, Nielsen A-M. (1998) Marginal production technologies for life cycle inventories. International Journal of Life Cycle Assessment 4(1):48-56